梅涅劳斯（Menelaus）定理（简称梅氏定理）最早出现在由古希腊数学家梅涅劳斯的著作《球面学》（Sphaerica）中。一条截线在三角形各边上确定出的六条线段，三条不连续线段的乘积等于剩下三条线段的乘积。这一定理同样可以轻而易举地用初等几何或通过应用简单的三角比关系来证明。梅涅劳斯把这一定理扩展到了球面三角形。

发展简史

梅涅劳斯是公元一世纪希腊数学家和天文学家．他解决了一个很重要的问题——共线点问题，通称为梅涅劳斯定理。

定理定义

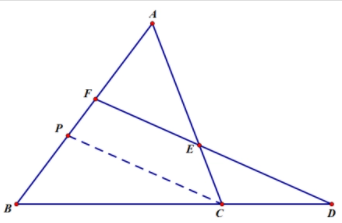
当一条直线交三边所在的直线分别于点时，则有

验证推导

证明一

过点A作交的延长线于点。则

证明二

过点作交于，则

两式相乘得

证明三

过点作的垂线，垂足为点，延长交边的延长线于点，连接，则，所以，且，在中，由结论1可知，代入已知条件可得，即为。

证明四：

不妨设，交于点，交于点，交于点，记，，，

由结论2可得：

从而，，三线共点

是同一点

证明五

作平行于交于点

定理推广

梅涅劳斯定理在三角形中成立，我们同样可以推广到三棱锥中去，也同样能得出优美的定理．并且能有很好的应用

分别是正四面体的棱上的点，则四点共面的充要条件是： 

。

不妨设相交于一点，在面和中，梅涅劳斯定理知：

若不共面．但是可确定一个平面．交于一点，则由“必要性“知：

命题可看作“梅涅劳斯定理”在空间四面体中的推广。

定理意义

在证明平面几何题时，常常需要将所要证明的结论进行转化，归结为基本几何图形——三角形。本文从课本上一道习题出发，将其推广为三角形中的一个等量表达式。

它反映了三角形中各种线段之间的关系，对于解决许多有关三角形中线段的问题，往往能起到事半功倍的效。比如塞瓦定理和梅涅劳斯定理就可以通过本文的结论简单推出，三角形中的内外角平分线性质也可以得到一个有趣的证明，等等。尤其在做自招题和数学竞赛试题中，该等式非常有用。