公式法是解一元二次方程的一种方法,也指套用公式计算某事物。
另外还有配方法、十字相乘法、直接开平方法与分解因式法等解方程的方法。公式表达了用配方法解一般的一元二次方程的结果。
根据因式分解与整式乘法的关系,把各项系数直接带入求根公式,可避免配方过程而直接得出根,这种解一元二次方程的方法叫做公式法。
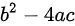
步骤
- 化方程为一般式:
- 确定判别式,计算Δ(希腊字母,音译为德尔塔)。
- 若Δ>0,该方程在实数域内有两个不相等的实数根:
若Δ=0,该方程在实数域内有两个相等的实数根:
若Δ<0,该方程在实数域内无解,但在虚数域内有两个共轭复根,为
证明
任何一元二次方程都能写成一般形式:
①
运用配方法能否解出①呢?
移项,得
二次项系数化1,得
配方
即
∵a≠0
∴4a2>0
的值有三种情况:
1)
由②得
∴
2)
由②得
3)
由②得<0
∴实数范围内,此方程无解
根的判别式
一般的,式子叫做方程的判别式,通常用希腊字母Δ表示它,即
如果,则这个一元二次方程有两个不同的实数根。
如果,则这个一元二次方程有两个相等的实数根。
如果,则这个一元二次方程有两个不同的复数根,且为共轭复根。这时根为
(其中)
求根公式
综上所述,当Δ≥0时,方程的实数根可写为
(蓝色部分称为根的判别式)
这个式子叫做一元二次方程的求根公式,通过求根公式可知,一元二次方程的根只可能有两个(有相同的算两个)。
注意事项
一定不会出现不能用公式法解一元二次方程的情况。
但在能直接开方或者因式分解时最好用直接开方法和分解因式法。
该文章由作者:【在山的那一边】发布,本站仅提供存储、如有版权、错误、违法等相关信息请联系,本站会在1个工作日内进行整改,谢谢!
