中位线是在三角形或梯形中一条特殊的线段,与其所在的三角形或梯形有着特殊的关系。连接三角形的两边中点的线段叫做三角形的中位线。三角形有三条中位线,首尾相接时,每个小三角形面积都等于原三角形的四分之一,这四个三角形都互相全等。平行线等分线段定理是把一条线段任意等分的重要依据。
定理内容
如果一组等距的平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等,经过三角形一边中点且与另一边平行的直线必平分第三边经过梯形一腰的中点且与底边平行的直线必平分另一腰,第二条定理也做:三角形过一边中点的直线平行第二边平分第三边。也称“一二三定理”。第二第三条即常说的“中位线定理”。
证明过程
证明如下:
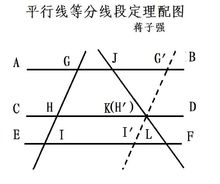
已知:AB∥CD∥EF,GI,JL交AB,CD,EF于点G,J,H,K,I,L.(如右图)
求证:GH:HI=JK:KL
证明:
过点K作G'I'∥GI交AB,CD,EF于点G',H'I'.
∵AB∥CD∥EF,G'I'∥GI
∴四边形GHKG',HII'H‘,GII'G是平行四边形(平行四边形判定定理),∠BJK=∠KLI,∠JG'I'=∠G'I'F(内错角相等)
∴△JG'K∽△I'LK,(相似三角形判定),GH=G'H',HI=H'I'(平行四边形对边相等)
∵G'H':H'I'=JK:KL(相似三角形性质)
∴GH:HI=JK:KL(等量代换)
推论1:过三角形一边中点与另一边平行的直线必平分第三边
推论2:过梯形一腰中点且平行于底边的直线必过另一腰中点
该文章由作者:【经济学家茶座】发布,本站仅提供存储、如有版权、错误、违法等相关信息请联系,本站会在1个工作日内进行整改,谢谢!
