分母有理化是数学上的专有名词,指的是通过适当的变形化去代数式分母中根号的运算。分母有理化(fēn mǔ yǒu lǐ huà)(Rationalize the denominator),又称"有理化分母",指的是在二次根式中分母原为无理数,而将该分母化为有理数的过程,也就是将分母中的根号化去。
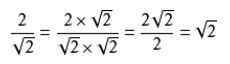
概述
由于在初中、高中阶段,最后的二次根式结果要求分母不含根号,故分母有理化成为初中学生学习和使用的一种重要方法。
将分母有理化,会使根式的运算变得简便。
常规方法
下面介绍两种分母有理化的常规方法,基本思路是把分子和分母都乘以同一个适当的代数式,使分母不含根号。
分母是一个单项式
例如二次根式,下面将之分母有理化:
分子分母同时乘以√2,分母变为2,分子变为2√2,约分后,分数值为√2。在这里我们想办法把√2化为有理数,只要变为它的平方即可。
分母是一个多项式
思路仍然是将分子分母同乘相同数。这里使用平方差公式,同时乘上√2+1,分子变为2√2+2,分数值为2√2+2,再约分即可。也就是说,为了有理化多项式的分母,原来分母是减号,我们乘上一个数字相同但用加号连接的式子,再用平方差公式。去分母时.如果分子是一个多项式.应加并且要注意不等式两边的每一项都乘以各分母。
特殊方法
下面有一些特殊的方法供参考!
分解约简法
将分母有理化:
这里我们将分母分解因式后提取出来,这样避免采用平方差公式分解。这种方法较适用于分子分母含有公因式时。
配方约简法
将分母有理化:
这里我们将分子化成平方式,然后利用完全平方公式配方,再和分母约分,这样避免采用平方差公式分解。
注意事项
下面举一个含参数的二次根式:
将分母有理化:
在这里我们将分子用平方差公式分解因式,然后分解!注意在这里我们不能将分母乘以,因为有可能等于0,若分情况讨论又比较麻烦,此时我们就应该注意分子和分母的结构关系!
拓展
有理化因式
两个含有根式的代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式。
例如:
将分子、分母同时乘以分母的有理化因式。
有理化因式举例
如√a的有理化因式是正负√a,√a+√b的有理化因式是
√a-√b或√b-√a.
词语
分母有理化
fēn mǔ yǒu lǐ huà
释义
又称“有理化分母”。通过适当的变形化去代数式分母中根号的运算。在根式运算及把一个根式化成最简分式时,都要将分母有理化。
该文章由作者:【博思清】发布,本站仅提供存储、如有版权、错误、违法等相关信息请联系,本站会在1个工作日内进行整改,谢谢!
