在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
内容
三角形三边关系是三角形三条边关系的定则,具体内容是在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
一般
设三角形三边为a,b,c则
a+b>c,a>c-b
b+c>a,b>a-c
a+c>b,c>b-a
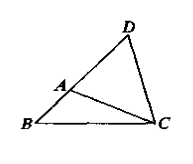
如图,
任意△ABC,求证AB+AC>BC。
证明:在BA的延长线上取AD=AC
则∠D=∠ACD(等边对等角)
∵∠BCD>∠ACD
∴∠BCD>∠D
∴BD>BC(大角对大边)
∵BD=AB+AD=AB+AC
∴AB+AC>BC
基本定理
1.任意两边之和大于第三边
2.任意两边之差小于第三边
设三角形三边为a,b,c则
a+b>c,a>c-b
b+c>a,b>a-c
a+c>b,c>b-a
三角形内角之和等于180度;大边对大角,大角对大边。
特别,在直角三角形中,两锐角之和等于90度,两直角边平方和等于斜边的平方。
该文章由作者:【奇数】发布,本站仅提供存储、如有版权、错误、违法等相关信息请联系,本站会在1个工作日内进行整改,谢谢!
